2 Research

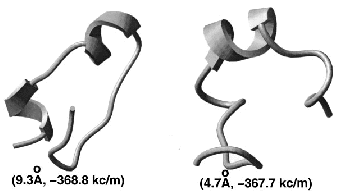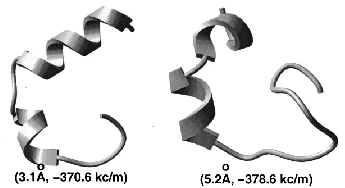Prediction of three-dimensional structures of proteins and peptides by global optimization of the free energy estimate has been attempted without much success for over thirty years. The key problems were the insufficient accuracy of the free energy estimate and the giant size of the conformational space. Global optimization of the free energy function of a peptide in internal coordinate space is a powerful method of structure prediction that out-performs both Molecular Dynamics, bound by the continuity requirement, and Monte Carlo, bound by the Boltzmann ensemble gener-ation requirement. We demonstrate that stochastic global optimization algorithms of the first order, i.e., with local minimization after each iteration (e.g., Monte Carlo-Minimization), have a greater chance of finding the global minimum after a fixed number of function evaluations. Recently, the principle of optimal bias was mathematically justified and the Optimal-Bias Monte Carlo-Minimization algorithm (a.k.a. Biased Probability Monte Carlo-minimization) was successfully applied to theoretical ab initio folding of several peptides, resulting in more than a 10-fold increase in efficiency compared to the Monte Carlo-Minimization method. 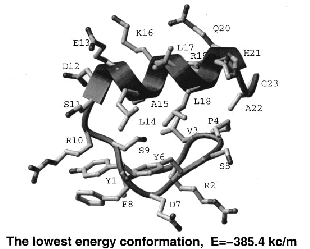The square-root bias is shown to be comparable in performance with the previously derived linear bias. A 23-residue peptide of beta-beta-alpha structure can be predicted from any random starting conformation.

[J.Computational Physics - 1999] [PDF]