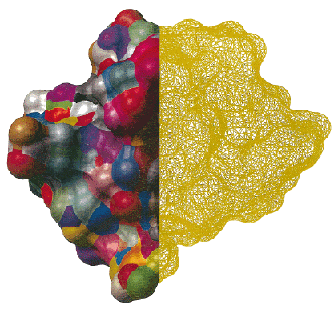2 Research

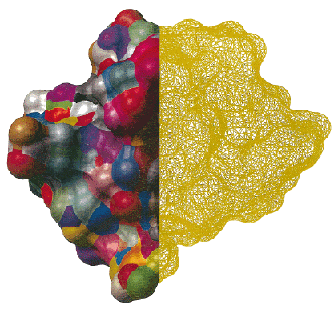The composite boundary elements compared to the basic triangles. Left half of the molecular surface of the polypeptide (shown in solid) has composite boundary elements colored randomly to illustrate the distribution of sizes and shapes. Right half of the molecular surface is displayed as a mesh directly produced by triangulation procedure. Drastic difference in the number of surface elements can be observed.

Solvation effects play a profound role in the energetics of protein folding. While a continuum dielectric model of solvation may provide a sufficiently accurate estimate of the solvation effects, until now this model was too computationally expensive and unstable for folding simulations. Here we proposed a fast yet accurate and robust implementation of the boundary element solution of the Poisson equation, the REBEL algorithm. Using our earlier double-energy scheme, we included for the first time the mathematically rigorous continuous REBEL solvation term in our Biased Probability Monte Carlo (BPMC) simulations of the peptide folding. The free energy of a 23-residue betabetaalpha-peptide was then globally optimized with and without the solvation electrostatics contribution. An ensemble of betabetaalpha conformations was found at and near the global minimum of the energy function with the REBEL electrostatic solvation term. Much poorer correspondence to the native solution structure was found in the "control" simulations with a traditional method to account for solvation via a distance-dependent dielectric constant. Each simulation took less than 40 h (21 h without electrostatic solvation calculation) on a single Alpha 677 MHz CPU and involved more than 40,000 solvation energy evaluations. This work demonstrates for the first time that such a simulation can be performed in a realistic time frame. The proposed procedure may eliminate the energy evaluation accuracy bottleneck in folding simulations.

[Biopolymers - 2001] [PDF]