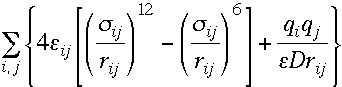Treatment of the nonbonded energy termsThe most time consuming part of a molecular dynamics simulation is the calculation of the nonbonded terms in the potential energy function, e.g., the electrostatic and van der Waals forces.
In principle, the non-bonded energy terms between every pair of atoms should be evaluated; in this case, the number of increases as the square of the number of atoms for a pairwise model (N2). To speed up the computation, the interactions between two atoms separated by a distance greater than a pre-defined distance, the cutoff distance, are ignored. Several different ways to terminate the interaction between two atoms have been developed over the years; some work better than others.
[clic on the figure to see a larger version] Truncation: the interactions are simply set to zero for interatomic distances greater than the cutoff distance. This method can lead to large fluctuations in the energy. This method is not often used. The SHIFT cutoff method: this method modifies the entire potential energy surface such that at the cutoff distance the interaction potential is zero. The drawback of this method is that equilibrium distances are slightly decreased. The SWITCH cutoff method: This method tapers the interaction potential over a predefined range of distances. The potential takes its usual value up to the first cutoff and is then switched to zero between the first and last cutoff. This model suffers from strong forces in the switching region which can slightly perturb the equilibrium structure. The SWITCH function is not recommended when using short cutoff regions.
|
| References
Allen, M. P. and D. J. Tildesley (1989). Computer Simulation of Liquids, Oxford University Press. Alper, H. E. and R. M. Levy (1989). Computer simulations of the dielectric properties of water: Studies of the simple point charge and transferrable intermolecular potential models. J. Chem. Phys. 91(2): 1242-1251. Brooks, B. R., R. E. Bruccoleri, et al. (1983). CHARMM: A Program for Macromolecular Energy Minimization and Dynamics Calculations.; J. Comp. Chem 4: 187-217. Greengard, L. and V. Rokhlin (1987). A Fast Algorithm for Particle Simulations. J. Comp. Phys. 73: 325-348. Pantoliano, M. W., M. Whitlow, et al. (1988). The Engineering of Binding Affinity at Metal Ion Binding Sites for the Stabilization of Proteins: Subtilisin as a Test Case.; Biochemistry 27: 8311-8317. Russell, A. J. and A. R. Fersht (1987). Rational modification of enzyme catalysis by engineering surface charge.; Nature 328: 496-500. Shimada, J., H. Kaneko, et al. (1994). Performance of fast multipole methods for calculating electrostatic. J. Comp. Chem 15(1): 28-43. Stote, R. H. and M. Karplus (1995). Zinc Binding in Proteins and Solution: A Simple but Accurate Nonbonded Representation, Proteins: Struct. Func. Gen. 23: 12-31. Stote, R. H., D. J. States, et al. (1991). On the treatment of electrostatic interactions in biomolecular simulation. J. Chim. Phys. 88: 2419-2433. Straub, J. E., C. Lim, et al. (1994). Simulation Analysis of the Binding Interactions in the RNase A/3'-UMP Enzyme-Product Complex as a function of pH. j. Am. Chem. Soc. 116: 2591-2599. Thomas, P. G., A. J. Russel, et al. (1985). Tailoring the pH dependence of enzyme catalysis using protein engineering. Nature 318: 375-376. York, D. M., T. A. Darden, et al. (1993). The effect of long-range electrostatic interactions in simulations of macromolecular crystals: a comparison of the Ewald and truncated list methods. J. Chem. Phys. 99: 8345-8348. |
The Extended Electrostatics Model
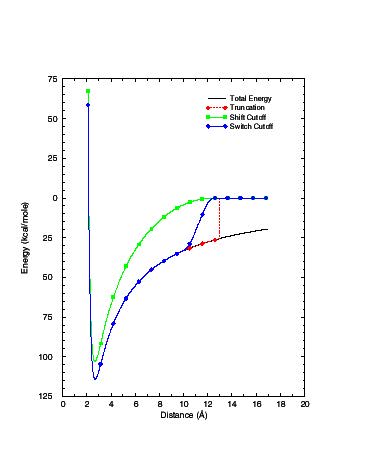
The Extended Electrostatics model approximates the full electrostatic interaction by partitioning the electric potential and the resulting forces on the atom at Ri into a "Near" and an "Extended" contribution. The "Near" contribution arises from the charged particles which fall within the sphere defined by the cutoff distance Rcut, while the "Extended" contribution, arises from the particles which are beyond the cutoff distance Rcut. The "Near" contribution is calculated by a conventional pairwise sum and the "Extended" contribution to the potential at Ri is calculated using a multipole approximation (Stote, States et al. 1991).
Treatment of Solvent in a Molecular Dynamics Simulation
Solvent, usually water, has a fundamental influence on the structure, dynamics and thermodynamics of biological molecules, both locally and globally. One of the most important effects of the solvent is the screening of electrostatic interactions. The electrostatic interaction between two charges is given by Coulomb’s law,
![]()
where qi, qj are the partial atomic charges, eelec is the effective dielectric constant and rij is the relative distance between the two particles. It is important to include solvent effects in an MD simulation. This can be done at several levels. The simplest treatment is to simply include a dielectric screening constant in the electrostatic term of the potential energy function. In this implicit treatment of the solvent, water molecules are not included in the simulation but an effective dielectric constant is used. Often the effective dielectric constant is taken to be distance dependent, eeff=rije), where e ranges from 4 to 20. Although this is a crude approximation, it is still much better than using unscreened partial charges. Other implicit solvent models have been developed that range from the relatively simple distance-dependent dielectric constants to models that base the screening on the solvent exposed surface area of the protein. The distance-dependent dielectric coefficient is the simplest way to include solvent screening without including explicit water molecules and it is available in most simulation programs. Recently, several implicit solvent models based on continuum electrostatic theory have been developed {ref}.
If water molecules are explicitly included in the simulation, then e = 1 in the energy function; the explicit water molecules provide the electrostatic shielding. In this more detailed treatment of the solvent boundary conditions must be imposed, first, to prevent the water molecules from diffusing away from the protein during the simulation, and second to allow simulation and calculation of macroscopic properties using a limited number of solvent molecules. Several different treatments of the boundary exist, the use of one over another depends strongly on the type of problem the simulation is to address.
Periodic Boundary conditions
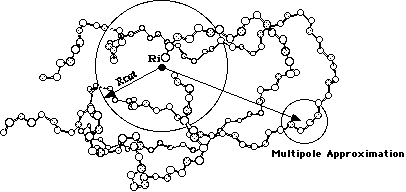
Periodic boundary conditions enable a simulation to be performed using a relatively small number of particles in such a way that the particles experience forces as though they were in a bulk solution. See, for example, the two dimensional box. The central box is surrounded by eight neighbors. The coordinates of the image particles, those found in the surrounding box are related to those in the primary box by simple translations. The simplest box is the cubic box. Forces on the primary particles are calculated from particles within the same box as well as in the image box. The cutoff is chosen such that a particle in the primary box does not see its image in the surrounding boxes.
Solvation shells
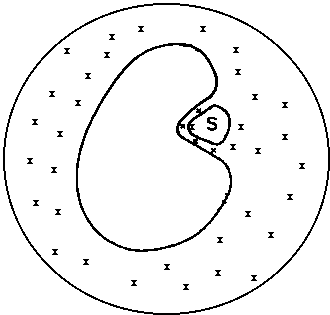
There exist numerous cases where one may not wish to use periodic boundary conditions. In some cases, the use of periodic boundary conditions requires the use of a prohibitively large number of water molecules.
With the increase in computer power, it has become much more feasible to incorporate water molecules in the simulation. The simplest way is to surround the protein or just a part of the protein with a sphere of water. Boundary potentials have been developed which restrain the water molecules to a sphere while maintaining a strong semblence to bulk water. Structural and thermodynamics properties when calculated under these conditions indicate that the water still behaves as bulk water. This usually involves much fewer water molecules than in a periodic boundary simulation and is often sufficient.
Active site solvation
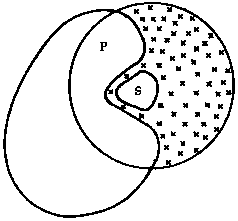
Often in the case of proteins, in particular enzymes, there is a large protein scafold yet one is primarily interested in what is happening in the active site. In this case, the enzyme can be partitioned into several regions. The reaction zone corresponds to that part of the enzyme which is of interest, usually the active site. Everything outside the reaction zone is referred to as the reservoir region. Atoms in the reservoir region are usually held fixed or harmonically constrained. The reaction zone is then solvated with a sufficiently large sphere of water and only this region is allowed to move during a molecular dynamics simulation. This allows for a significant speed up of computer time if one is just interested in a localized region.
Setting up and running a Molecular Dynamics Simulations
In a molecular dynamics simulation, the time dependent behavior of the molecular system is obtained by integrating Newton’s equations of motion using one of the numerical integrators described earlier (see Classical Mechanics) and the potential energy function (see Potential Energy Function). The result of the simulation is a time series of conformations; this is called a trajectory or the path followed by each atom in accordance with Newton’s laws of motion. Most molecular dynamics simulations are performed under conditions of constant N,V,E (the microcanonical ensemble), but more recent methods perform simulations at constant N, T and P to better mimic experimental conditions. In this section we describe in some detail the steps taken to setup and run a molecular dynamics simulation.
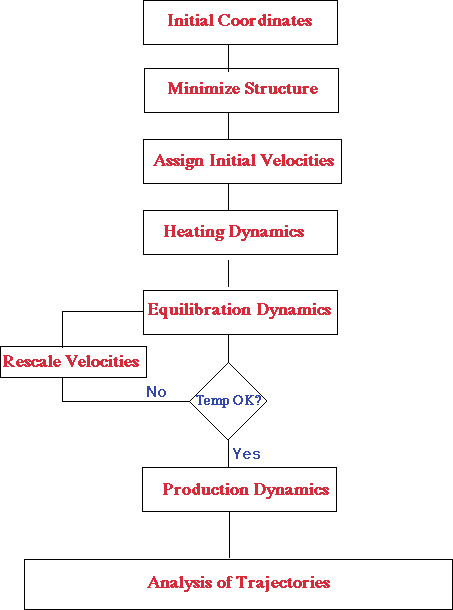
Initialization
To begin a molecular dynamics simulation, you must first choose an initial configuration of the system, a starting point, or t=0. Most often, in simulations of biomolecules, an x-ray crystal structure or an NMR structure is obtained from the Brookhaven Protein Databank (http://www.rcsb.org/pdb/) and used as the initial structure. It is also possible to use a theoretical structure developed by homology modeling. The choice of the initial configuration must be done carefully as this can influence the quality of the simulation. It is often good to choose a configuration close to the state that you wish to simulate.
Prior to starting a molecular dynamics simulation, it is advisable to do an energy minimization of the structure. This removes any strong van der Waals interactions that may exisit, which might otherwise lead to local structural distortion and result in an unstable simulation.
At this point, explicit water molecules are added to solvate the protein. If you are starting from an x-ray crystal structure, then it is likely that some water molecules are already present, but the amount is usually insufficient for solvation. The solvating water molecules are usually obtained from a suitable large box of water that has been previous equilibrated. The entire box of water is overlayed onto the protein and those water molecules that overlap the protein are removed. At this point, another energy minimization should be done with the protein fixed in its energy minimized position. This allows the water molecules to readjust to the protein molecule.
Heating the system
Initial velocities at a low temperature are assigned to each atom of the system and Newton’s equations of motion are integrated to propagate the system in time. If you are running an explicit solvent simulation, first fix the protein positions and let the waters move to adjust to the present of the protein. Once the waters are equilibrated, the constraints on the protein can be removed and the whole system (protein+water) can evolve in time. During the heating phase, initial velocities are assigned at a low temperature and the simulation is started. Periodically, new velocities are assigned at a slightly higher temperature and the simulation is allowed to continue. This is repeated until the desired temperature is reached.
Equilibration
Once the desired temperature is reached, the simulation of protein/water system continues and during this phase several properties are monitored; in particular, the structure, the pressure, the temperature and the energy. The point of the equilibration phase is to run the simulation until these properties become stable with respect to time. If the temperature increases or decreases significantly, the velocities can be scaled such that the temperature returns to near its desired value.
Production phase
The final step of the simulation is to run the simulation in "production" phase for the time length desired. This can be from several hundred ps to ns or more. It is during the production phase that thermodynamic parameters can be calculated so the simulation must conform to one of the ensembles described earlier.
Analysis of molecular dynamics simulations
When carrying out an MD simulation, coordinates and velocities of the system are saved; these are then used for the analysis. Time dependent properties can be displayed graphically, where one of the axis correpsonds to time and the other to the quantity of interest, such as energy, rmsd, etc. Other approaches have been developed for representing the time dependence of angle rotations (dihedrals). Average structures can be calculated and compared to experimental structures. Molecular dynamics simultions can help visualize and understand conformational changes at an atomic level when combined with molecular graphics programs which can display the structural parameters of interest in a time dependent way.
Some quantities that are routinely calculated from a molecular dynamics simulation include:
I)Mean Energy
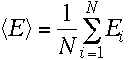
II)RMS difference between two structures
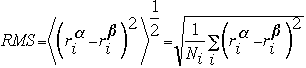
III)RMS fluctuations
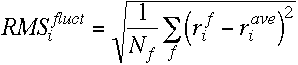
note the relation between the RMS fluctuations and the crystallographic B factors;
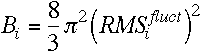
IV)radius of gyration
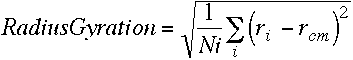
where ri - rcm is the distance between atom i and the center of mass of the molecule.
From a molecular dynamics simulation, time dependent properties such as correlation functions can also be calculated. These, in turn, can be related to spectroscopic measurement. We will not cover this aspect here.