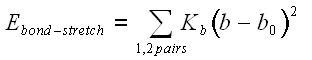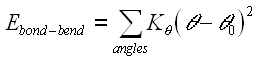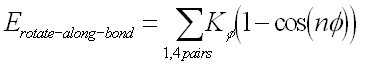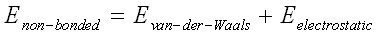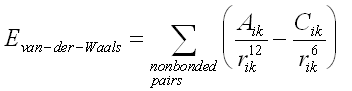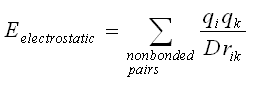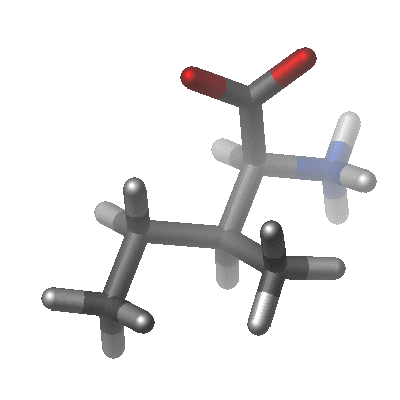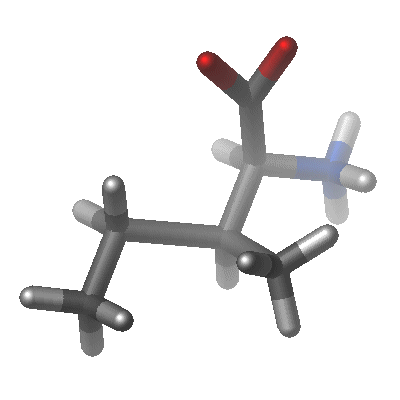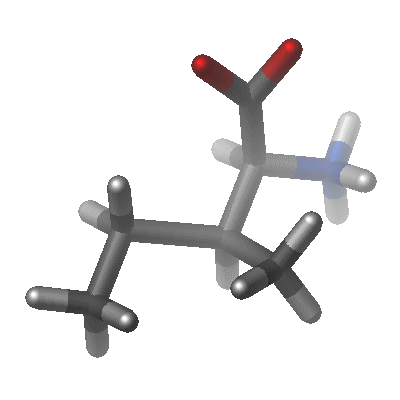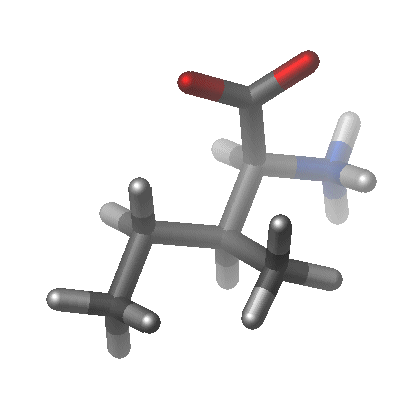
Theoretical studies of biological molecules permit the study of the relationships between structure, function and dynamics at the atomic level. Since many of the problems that one would like to address in biological systems involve many atoms, it is not yet feasible to treat these systems using quantum mechanics. However, the problems become much more tractable when turning to empirical potential energy functions, which are much less computationally demanding than quantum mechancis; but this comes at a cost. Numerous approximations are introduced which lead to certain limitations. These are discussed below. Current generation force fields (or potential energy functions) provide a reasonably good compromise between accuracy and computational efficiency. They are often calibrated to experimental results and quantum mechanical calculations of small model compounds. Their ability to reproduce physical properties measurable by experiment is tested; these properties include structural data obtained from x-ray crystallography and NMR, dynamic data obtained from spectroscopy and inelastic neutron scattering and thermodynamic data. The development of parameter sets is a very laborious task, requiring extensive optimization. This is an area of continuing research and many groups have been working over the past two decades to derive functional forms and parameters for potential energy functions of general applicability to biological molecules. Among the most commonly used potential energy functions are the AMBER, CHARMM, GROMOS and OPLS/AMBER force fields. The continuing development of force fields remains an intense area of research with implications for both fundamental research as well as for applied research in the pharmaceutical industry. As mentioned above, there are certain limitations of empirical force fields. One of the most important is that no drastic changes in electronic structure are allowed, i.e., no events like bond making or breaking can be modeled. To address this limitation, mixed quantum mechanical - molecular mechanical force fields are under development in a number of laboratories. We will not cover these force fields in the current manual. Complete potential functions are now available for macromolecular simulations; one particular example is the CHARMM22 all atom potential function for proteins (MacKerell et al 1998), nucleic acids (MacKerell et al. 1995), lipids (Schlenkrich et al. 1996) and carbohydrates (Ha et al. 1988). References A. D. MacKerell Jr., J. Wiórkiewicz-Kuczera, and M. Karplus (1995). An All-Atom Empirical Energy Function for the Simulation of Nucleic Acids, J. Am. Chem. Soc. 117, 11946-11975. A. D. MacKerell, Jr., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin, M. Karplus (1998). All-atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. 102, 3586-3616. M. Schlenkrich, J. Brickmann, A. D. MacKerell Jr., and M. Karplus (1996). An Empirical Potential Energy Function for Phospholipids: Criteria for Parameter Optimization and Applications, in Biological Membranes: A Molecular Perspective from Computation and Experiment, K. M. Merz, Jr. and B. Roux, editors (Birkhauser), 31-81. S.N. Ha, A. Giammona, M. Field, J.W. Brady, A revised potential-energy surface for molecular mechanics studies of carbohydrates, Carbohydr. Res. (1988), 180(2), 207-221. The CHARMM potential energy function The energy, E, is a function of the atomic positions, R, of all the atoms in the system, these are usually expressed in term of Cartesian coordinates. The value of the energy is calculated as a sum of internal, or bonded, terms Ebonded, which describe the bonds, angles and bond rotations in a molecule, and a sum of external or nonbonded terms, Enon-bonded, These terms account for interactions between nonbonded atoms or atoms separated by 3 or more covalent bonds. The Ebonded term is a sum of three terms: which correspond to three types of atom movement: The first term in the above equation is a harmonic potential representing the interaction between atomic pairs where atoms are separated by one covalent bond, i.e., 1,2-pairs. This is the approximation to the energy of a bond as a function of displacement from the ideal bond length, b0. The force constant, Kb, determines the strength of the bond. Both ideal bond lengths b0 and force constants Kb are specific for each pair of bound atoms, i.e. depend on chemical type of atoms-constituents. Values of force constant are often evaluated from experimental data such as infrared stretching frequencies or from quantum mechanical calculations. Values of bond length can be inferred from high resolution crystal structures or microwave spectroscopy data. The second term in above equation is associated with alteration of bond angles theta from ideal values q0 , which is also represented by a harmonic potential. Values of q0 and Kq depend on chemical type of atoms constituting the angle. These two terms describe the deviation from an ideal geometry; effectively, they are penalty functions and that in a perfectly optimized structure, the sum of them should be close to zero.

The third term represents the torsion angle potential function which models the presence of steric barriers between atoms separated by 3 covalent bonds (1,4 pairs). The motion associated with this term is a rotation, described by a dihedral angle and coefficient of symmetry n=1,2,3), around the middle bond. This potential is assumed to be periodic and is often expressed as a cosine function. In addition to these term, the CHARMM force field has two additional terms; one is the Urey-Bradley term, which is an interaction based on the distance between atoms separated by two bond (1,3 interaction). The second additional term is the improper dihedral term (see the section on CHARMM) which is used to maintain chirality and planarity. The parameters for the these terms, Kb, Kq, Kf, are obtained from studies of small model compounds and comparisons to the geometry and vibrational spectra in the gas phase (IR and Raman spectroscopy), supplemented with ab initio quantum calculations. The energy term representing the contribution of non-bonded interactions in the CHARMM potential function has two components, the Van der Waals interaction energy and the electrostatic interaction energy. Some other potential functions also include an additional term to account for hydrogen bonds. In the CHARMM potential energy function, these interactions are account for by the eleedctrostatic and Van der Waals interactions. 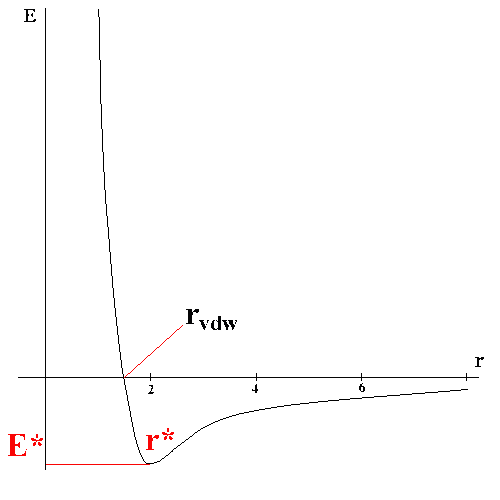The van der Waals interaction between two atoms arises from a balance between repulsive and attractive forces. The repulsive force arises at short distances where the electron-electron interaction is strong. The attractive force, also referred to as the dispersion force, arises from fluctuations in the charge distribution in the electron clouds. The fluctuation in the electron distribution on one atom or molecules gives rise to an instantaneous dipole which, in turn, induces a dipole in a second atom or molecule giving rise to an attractive interaction. Each of these two effects is equal to zero at infinite atomic separation r and become significant as the distance decreases. The attractive interaction is longer range than the repulsion but as the distance become short, the replusive interaction becomes dominant. This gives rise to a minimum in the energy. Positioning of the atoms at the optimal distances stabilizes the system. Both value of energy at the minimum E* and the optimal separation of atoms r* (which is roughly equal to the sum of Van der Waals radii of the atoms) depend on chemical type of these atoms. The van der Waals interaction is most often modelled using the Lennard-Jones 6-12 potential which expresses the interaction energy using the atom-type dependent constants A and C. Values of A and C may be determined by a variety of methods, like non-bonding distances in crystals and gas-phase scattering measurements The van der Waals interactions are one of the most important for the stability of the biological macromolecules. The electrostatic interaction between a pair of atoms is represented by Coulomb potential; D is the effective dielectric function for the medium and r is the distance between two atoms having charges qi and qk. The empirical potential energy function is differentiable with respect to the atomic coordinates; this gives the value and the direction of the force acting on an atom and thus it can be used in a molecular dynamics simulation. The empirical potential function has several limitations, which result in inaccuracies in the calculated potential energy. One limitation is due to the fixed set of atom types employed when determining the parameters for the force field. Atom types are used to define an atom in a particular bonding situation, for example an aliphatic carbon atom in an sp3 bonding situation has different properties than a carbon atom found in the His ring. Instead of presenting each atom in the molecule as a unique one described by unique set of parameters, there is a certain amount of grouping in order minimize the number of atom types. This can lead to type-specific errors. The properties of certain atoms, like aliphatic carbon or hydrogen atoms, are less sensitive to their surroundings and a single set of parameters may work quite well, while other atoms like oxygen and nitrogen are much more influenced by their neighboring atoms. These atoms require more types and parameters to account for the different bonding environments. An approximation introduced to decrease the computational demand is the pair-wise additive approximation, i.e., interaction energy between one atom and the rest of the system is calculated as a sum of pair-wise (on atom to one atom) interactions, or as if the pair of atoms do not see the other atoms in the system. The simultaneous interaction between three or more atoms is not calculated, so certain polarization effects are not explicitly included in the force field. This can lead to subtle differences between calculated and experimental results, for example, in the calculation of experimentally observable pK shifts of ionizable amino acid residue side chains induced by electrostatic field of the whole protein . Another important point to take into consideration is that the potential energy function does not include entropic effects. Thus, a minimum value of E calculated as a sum of potential functions does not necessarily correspond to the equilibrium, or the most probable state; this corresponds to the minimum of free energy. Because of the fact that experiments are generally carried out under isothermal-isobaric conditions (constant pressure, constant system size and constant temperature) the equilibrium state corresponds to the minimum of Gibb's Free Energy, G. While just an energy calculation ignores entropic effects, these are included in a molecular dynamics simulations