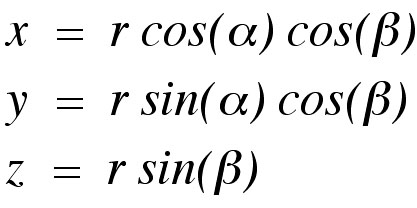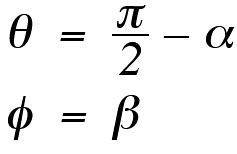The alpha-release of DOT includes a set of rotations
which can be used to rotate the moving molecule. To represent rotations in a compact form, we used Eulerian angles in ZXZ convention. According to our convention, the rotation matrix for an Eulerian angle ,
has the following form:
,
has the following form:
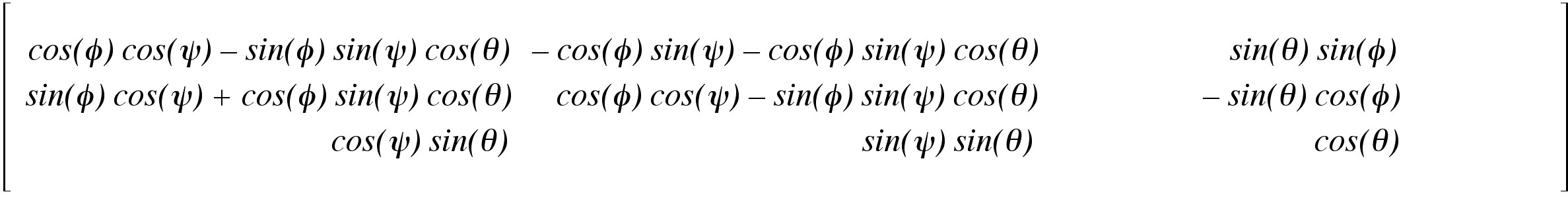
Note that some references give the Eulerian angles in the
order 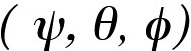 , to denote
that the first rotation (about the z-axis) is given by the
angle
, to denote
that the first rotation (about the z-axis) is given by the
angle 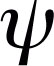 , the second rotation
(about the x-axis) is given by the angle
, the second rotation
(about the x-axis) is given by the angle
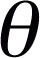 ,
and the final rotation (about the z-axis) is given the the angle
,
and the final rotation (about the z-axis) is given the the angle
 . The angle
. The angle 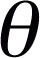 ranges from 0 to
ranges from 0 to  radians, while
radians, while
 and
and 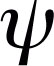 range from 0 to 2
range from 0 to 2 radians.
radians.
The alpha-release of DOT is supplied with 3 rotation files:
6x6.euler
- 6 by 6 degree rotations for big molecules,
12x12.euler - 12 by 12 degree
rotations for medium-size molecules,
20x20.euler - 20 by 20 degree
rotations for small molecules.
The user may run DOT with the supplied files or generate
customized rotation samples, tuned to the moving molecule size.
The following table contains rough estimates of
the angular increment (degrees) as a function of the moving molecule radius (Angstroms), assuming 1 Å grid resolution:
Radius (Å) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Increment (degrees) |
60 |
29 |
19.2 |
14.4 |
11.5 |
9.6 |
8.2 |
7.2 |
6.4 |
5.7 |
5.2 |
4.8 |
4.4 |
4.1 |
3.8 |
3.6 |
3.4 |
3.2 |
3.0 |
2.9 |
Note: angle generation utilities will be available
with the beta release of DOT. Alpha testers desiring angular
samples other than those provided are encouraged to contact
the CCMS directly at ccms-help@sdsc.edu.
The generation of a rotation sample is done in two stages:
Step 1: Create a set of uniformly distributed points on the sphere.
This set is generated by the repulsion utility.
To run this utility, type:
repulsion angle > repulsion_output_file
were parameter angle (in degrees) specifies the
lower limit for the angular distance between any point and its closest neighbors on the unit sphere. The repulsion_output_file will contain a set of
uniformly distributed unit vectors, represented by their X, Y, and Z coordinates.
Step 2: Create a set of Euler angles using the set of
points on the sphere. The angles are generated by dot_gen_rots utility.
To run this utility, type:
dot_gen_rots angle <
repulsion_output_file > euler_output_file
were parameter angle (in degrees) specifies the
angular increment. We suggest using the same angular increment for
input into repulsion and dot_gen_rots, although
the user may find it useful to set these angular steps independently.
The algorithm proceeds by using the spherical coordinates
of the given points on the sphere to define the Euler angles
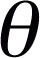 and
and  . If one examines the
third column of the rotation matrix (which incidentally is
the image of the point (0,0,1) under the rotation), one
sees that it has the same structure as the standard definition
of spherical coordinates
. If one examines the
third column of the rotation matrix (which incidentally is
the image of the point (0,0,1) under the rotation), one
sees that it has the same structure as the standard definition
of spherical coordinates
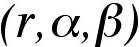 , where a point on the sphere is defined according to
the formulas:
, where a point on the sphere is defined according to
the formulas:
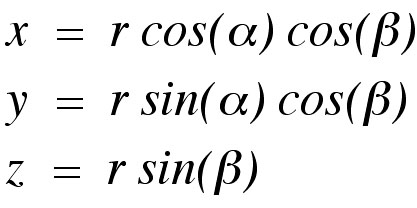
By setting
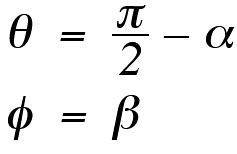
we see that the spherical
coordinates of the points on the sphere serve to define the
angles 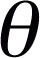 and
and  . In order to give a uniform rotational sampling, the angle
. In order to give a uniform rotational sampling, the angle 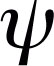 is chosen to be of the form
is chosen to be of the form

k = 1, 2, ...
![]() ,
has the following form:
,
has the following form:
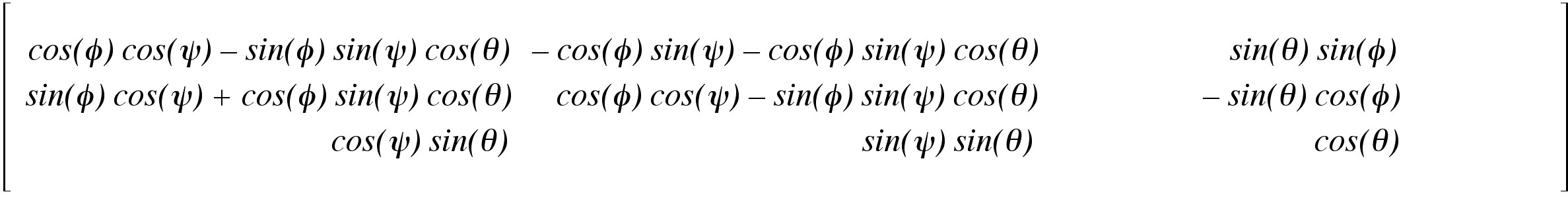
![]() , to denote
that the first rotation (about the z-axis) is given by the
angle
, to denote
that the first rotation (about the z-axis) is given by the
angle ![]() , the second rotation
(about the x-axis) is given by the angle
, the second rotation
(about the x-axis) is given by the angle
![]() ,
and the final rotation (about the z-axis) is given the the angle
,
and the final rotation (about the z-axis) is given the the angle
![]() . The angle
. The angle ![]() ranges from 0 to
ranges from 0 to ![]() radians, while
radians, while
![]() and
and ![]() range from 0 to 2
range from 0 to 2![]() radians.
radians.