Blue, photoabsorption spectrum of helium gas after double-electron excitation. The solid line through the data points indicates the best fit. Red, spectrum calculated from theoretical model.

 Since the work of Poincaré a century ago, the problem of three bodies interacting under their mutual gravitational forces (such as the earth, moon, and sun) has been known to exhibit a mixture of classical and chaotic dynamics. A system of three charged particles should have similar dynamics (within a sign), even in very small systems. But as yet, scientists don't know how to reconcile chaos with a quantum mechanical view of the universe. Classical dynamics allows for the chaotic motion of three bodies, because the mechanics can be described with nonlinear equations of motion; quantum mechanics, however, does not have this way to account for chaos, because the Schrödinger equation is linear. Furthermore, the quantum states of the helium atom, the prototypical three-body charged-particle system, occur in seemingly regular progressions, labeled by sets of quantum numbers. How, then, can classical mechanics and quantum mechanics be reconciled? What are the manifestations of the underlying classical chaos in the quantum spectrum of helium?
 
 

Understanding Chaos

Those of us who are not physicists tend to think of chaos as a state of randomness, a complex situation where chance alone ultimately determines what is going on. For physicists, chaos is more ordered than random, and it shows up in seemingly simple systems. It is defined as an extreme sensitivity to initial conditions, to the point where small changes in these conditions lead to larger and larger differences in outcomes over time, ultimately yielding wildly divergent results. The result is a dynamic system whose future behavior we cannot predict by observation of its past behavior, even though its dynamics follow a set of determined rules. Systems like this are incredibly common. In fact, Henri Poincaré pointed out back in the 19th century that most dynamic systems are chaotic. Chaotic behavior has been noted in weather patterns, chemical reactions, and the evolution of insect populations. Studies of chaos help us to understand the behavior of earthquakes, lasers, fluids, mechanical structures, neural networks, and even biological rhythms. Thus, understanding chaos, both in the realm of the familiar classical mechanics and in the realm of quantum mechanics, is key to understanding the dynamics of our world.

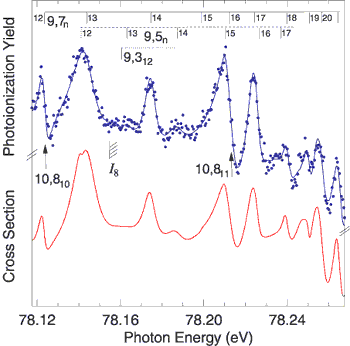
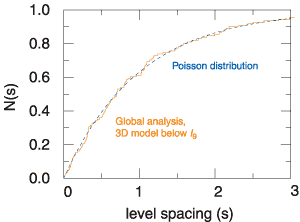
To answer these questions, an international group working at Beamline 9.0.1 (now Beamline 10.0.1) has used the bright beams of the ALS along with theoretical modeling to search for quantum chaos in the photoabsorption spectrum of helium—and they’ve found it. The high brightness on this undulator beamline allowed the resolution (about 2 meV) necessary to distinguish tightly spaced states near helium’s double-ionization threshold. Electrons in these high-energy, doubly excited states are known to show more classical behavior than those lying closer to the nucleus. But the states are so close together that a third-generation light source is needed to resolve them. The resulting spectrum was compared to a new theoretical model based on a random matrix approach to chaotic systems. Agreement between the model and the data was excellent, allowing the experimenters to extend the statistical analysis even to states above those seen in the experimental spectrum.

The electronic states of doubly excited helium can be labeled as N,K_n, where N is the principal quantum number of the inner electron, n is that of the outer electron, and K is the angular correlation between the two. States with the same N converge to an ionization threshold, I_N. The researchers found that, as the electron energies approach the ionization threshold for electrons with higher N, the statistical properties of the spacing between neighboring energy levels clearly display a transition toward quantum chaos. Where I_N >4, the N–1 series begins to be perturbed by higher series. Where I_N >8, the effect is strong enough that traditional quantum numbers can no longer describe the dynamics. Statistical analyses also showed that, as I_N increases, plots of the spacings between nearest-neighbor states move from being best described by a Poisson distribution (associated with regular systems) to more closely approximating a Wigner distribution (associated with chaotic systems). This observation of the onset of chaotic dynamics in a simple three-body system shows, for the first time, how the underlying classical chaos manifests in a simple and well-studied quantum system.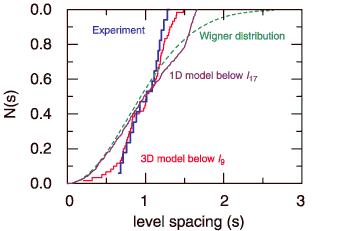

Cumulative distributions of nearest-neighbor spacings for the 1Po states of helium, analyzed individually for each series associated with a given value of N–K: blue, distribution derived from experiment; red, best fit from three-dimensional model calculations for states below I9; purple, best fit from one-dimensional model calculations for states below I17; dashed green line, Wigner distribution. The marked tendency toward a Wigner distribution as higher lying states are included indicates the onset of chaos.

Research conducted by R. Püttner, M. Domke, M. Martins, and G. Kaindl (Freie Universität Berlin), B. Grémaud and D. Delande (Université Pierre et Marie Curie), and A.S. Schlachter (Berkeley Lab).

Research funding: Deutsche Forschungsgemeinschaft, Bunderminister fuer Bildung und Forschung, and UMR 8552 of CNRS. Operation of the ALS is supported by the U.S. Department of Energy, Office of Basic Energy Sciences.

Publication about this research: R. Püttner, B. Grémaud, D. Delande, M. Domke, M. Martins, A.S. Schlachter, and G. Kaindl, "Statistical Properties of Inter-Series Mixing in Helium: From Integrability to Chaos," Phys. Rev. Lett. 86, 3747 (2001).

ALSNews Vol. 190, December 12, 2001